CS61A_Learning

CS61A-Learning Notes

[TOC]

WEEK 1

The first half week is mainly about how to use bash and how to use the OK system in website.

In the next half week, mostly it’s about python basic knowledge.

How to use git bash

  • ls: list all files
  • cd <path>: change the specified directory
  • mkdir <dir name>: to create a directory
  • mv <source file><destination path>: move a file
  • unzip <source file> : to unzip a file
  • winpyt python: to open the python edit space

How to use the OK system

  • python ok -q <qustion>: to test a specific question
  • python ok: to test all the question
  • python ok -v: to see how you did on all tests
  • python ok --local: to test it locally

How to use Python in bash

  • python3 example.py: it will run the code in the file you provide and return you to the command line.
  • python3 -i foo.py:The -i option runs your Python script, then opens an interactive session. In an interactive session, you run Python code line by line and get immediate feedback instead of running an entire file all at once.
  • python3 -m doctest foo.py: Runs doctests in a particular file. Doctests are surrounded by triple quotes (""") within functions.Each test in the file consists of >>> followed by some Python code and the expected output。

Python arithmetic expressions

  • Floating point division (/): divides the first number number by the second, evaluating to a number with a decimal point even if the numbers divide evenly.
  • Floor division (//): divides the first number by the second and then rounds down, evaluating to an integer.
  • Modulo (%): evaluates to the positive remainder left over from division.
1
2
3
4
5
6
7
8
>>> 7 / 4
1.75
>>> (2 + 6) / 4
2.0
>>> 7 // 4        # Floor division (rounding down)
1
>>> 7 % 4         # Modulus (remainder of 7 // 4)
3

The difference between Python and C++

when I learn C++, the if are like:

1
2
3
4
5
6
if(expression){
    <suite>;
    <suite>;
}else{
    <suite>;
}

But in Python it’s more like:

1
2
3
4
5
6
if <expression>:
    <suite>
elif <expression>:
    <suite>
else:
    <suite>

Pay attention to the elif .It’s different to the C++.And the expression part don’t need to have a ( ) But need have a:

The next it’s the while difference:

C++:

1
2
3
4
while(expression){
    <suite>;
    <suite>;
}

In Python it’s more like :

1
2
3
while <expression>:
    <suite>
    <suite>

About the function

It’s pretty familiar with C++ about the function. In Python it’s like this one:

1
2
3
def <name>(<formal parameters>):
    
    return <return expression>

Here is a good example:

1
2
3
4
5
6
7
8
from operator import add, mul

def square(x):
	    return mul(x, x)	
def sum_squares(x, y):
		return add(square(x), square(y))
	
result = sum_squares(5, 12)

In C++, we execute every codes by main function. It’s easy to define any variables. But in Python , things become a little bit unfamiliar.

1
2
3
4
5
6
7
x=12
z=7
def f(y):
    x=3
    print(x,y,z)
f(7)
print(x)

The code above is equal to C++ code below:

1
2
3
4
5
6
7
8
9
10
11
12
#include<iostream>
using namespace std;
int x=12,z=7;
int f(int y){
	int x=3;
	cout<<x<<" "<<y<<" "<<z<<endl;
}
int main(){
	f(7);
	cout<<x;
	return 0;
}

In Python we introduce a new concept: frame. There are two kind of frame: local frame and global frame. Every variables shows in a function called : this variables is in a local frame. And every variables shows right in Python we call it was in global frame.

The most important things is : when we try to find variables values we should follow the frame its in OR its up frame. :red_circle:

week 2

In the week Q&A video , some student ask one question about this topic.

1
2
3
4
>>> print(print (1),print(2))
1
2
None None

None Indicates that Nothing is Returned: The special value None represents nothing in Python . A function that does not explicitly return a value will return None.

1
2
3
4
>>> def does_not_return_square(x):
    	x * x
        
>>> does_not_return_square(4)

when we run the code above, nothing displayed. Because None is not displayed by the interpreter as the value of an expression.

1
2
>>> sixteen = does_not_return_square(4)
>>> sixteen + 4

If we run the code like above. The python will say:

File “”, line 1, in
TypeError : unsupported operand type(s) for +: ‘NoneType’ and ‘int’

The reason why the Python can’t add 4 to the sixteen because the None it’s not means 0,but it means another Type.

Pure Functions & Non-Pure Functions

This part is easy, so I just copy the picture in class:

Type Img
Pure Functions: just return values 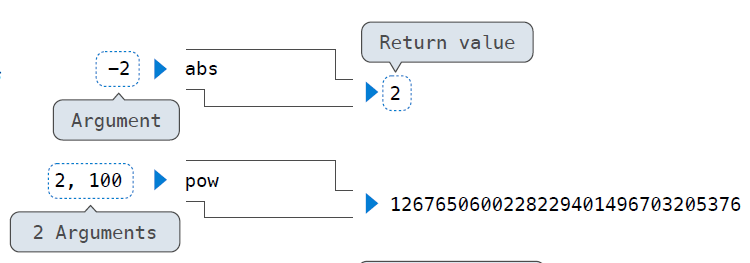image-20220506161307060
Non-Pure Functions: have side effects 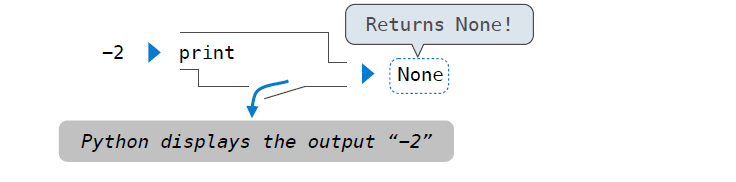image-20220506161320811

So the very first question can be see like this:

image-20220506161612929

Miscellaneous Python Features

Division:

When it comes to division, Python provides two infix operators: / and //. The former is normal division, so that it results in a floating point, or decimal value, even if the divisor evenly divides the dividend:

1
2
3
4
>>> 5 / 4
1.25
>>> 8 / 4
2.0

The // operator, on the other hand, rounds the result down to an integer:

1
2
3
4
>>> 5 // 4
1
>>> -5 // 4
-2

These two operators are shorthand for the truediv and floordiv functions.

1
2
3
4
5
>>> from operator import truediv, floordiv
>>> truediv(5, 4)
1.25
>>> floordiv(5, 4)
1

Multiple Return Values:

It works like this:

1
2
3
4
5
6
def operate(a, b):
    suma = a + b
    diff = a - b
    mul = a * b
    div = a / b
    return sum, diff, mul, div

And when we use it ,we do things like this:

1
suma, diff, mul, div = operate(n1, n2)

Doctests:

When we wrote a function ,we should leave a text about this function to let us know how this function worked.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#The file name is 01.py

def absolute_value(x):
    """Return the absolute value of X.

    >>> absolute_value(-3)
    3
    >>> absolute_value(0)
    0
    >>> absolute_value(3)
    3
    """
    if x < 0:
        return -x
    elif x == 0:
        return 0
    else:
        return x

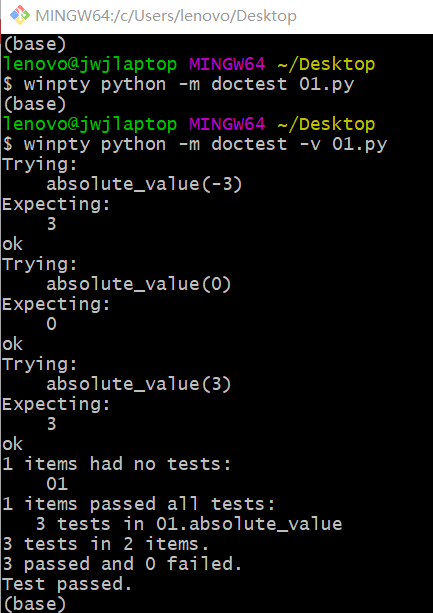
when we run the command like this:

1
winpty python -m doctest 01.py

There is nothing come out, that’s good. It means we passed all test. If we want to see more details, we use commands like this:

1
winpty python -m doctest -v 01.py

image-20220603222442691

Default Arguments:

When we called a function ,the value we give might not be exactly the function needs.We can the function a default values. This is not an assignment statement. This is a place holder for a value. Like this pieces below:

1
2
3
4
5
6
7
8
9
10
def divide_exact(n, d=10):
    """Return the quotient and remainder of dividing N by D.

    >>> quotient, remainder = divide_exact(618, 10)
    >>> quotient
    61
    >>> remainder
    8
    """
    return floordiv(n, d), mod(n, d)

It says if there’s no argument passed in to be bound to d then I’ll bind ten to d.

Error Messages:

Error Types Descriptions
SyntaxError Contained improper syntax (e.g. missing a colon after an if statement or forgetting to close parentheses/quotes)
IndentationError Contained improper indentation (e.g. inconsistent indentation of a function body)
TypeError Attempted operation on incompatible types (e.g. trying to add a function and a number) or called function with the wrong number of arguments
ZeroDivisionError Attempted division by zero

Designing Functions

There are three principles to design a function:

  1. Give each function exactly one job, but make it apply to many related situations.
  2. Don’t repeat yourself (DRY): Implement a process just once, but execute it many times.
  3. Define function generally.

One useful skills:

We can use assertstatement to alert poeple that we inputs the worong values.

1
2
3
4
5
>>> assert 3 > 2 , 'Math is bad'
>>> assert 3<2, 'Math is bad'
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
AssertionError: Math is bad

As we can see ,this python feather allows me to avoid the users inputs which I don’t want.

Functions as Arguments

The only things to understnd this part is to run this code in my mind:

1
2
3
4
5
6
7
8
9
10
11
12
13
def summation(n, term):
    total, k = 0, 1
    while k <= n:
        total, k = total + term(k), k + 1
    return total

def cube(x):
    return x*x*x

def sum_cubes(n):
    return summation(n, cube)

result = sum_cubes(3)

Functions as Return Values

In python we can defined function in the others functions body:

1
2
3
4
5
6
7
8
9
def make_adder(n):
"""Return a function that takes one argument k and returns k + n.
>>> add_three = make_adder(3)
>>> add_three(4)
7
"""
def adder(k):
	return k + n
return adder

When we run the codes above we know that the function return a function called adder. Let’s try to call this function like make adder(1) (2),It goes like that:

When we do Operator parts, we go like this:

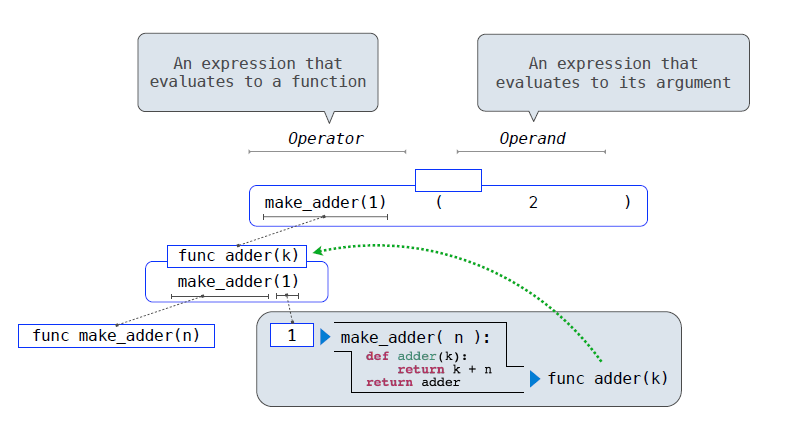
image-20220622160345778

The first part return a function adder(1),also it likes to call the adder function in this frame,in the end we got 3.

One things that need to pay attention is that when the computer execute the make_adder function,then execute.

In the next lecture this kind of function that return a function is called Self-Reference. Let’s see the code below:

1
2
3
4
5
def print_all(k):
    print(k)
    return print_all
    
print_all(1)(3)(5)

At each times, the print_all function return itself but it won’t be execute forever,it just return and rebind. The execute steps are like:

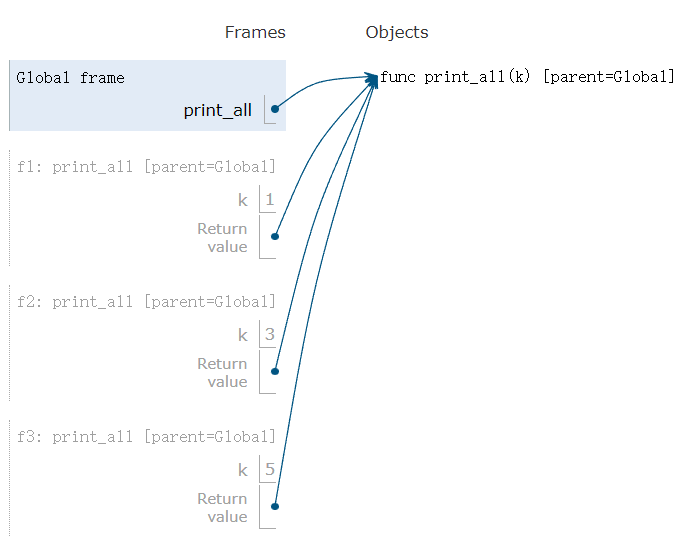
image-20220628141744467

Another things need to pay attention is that : this feature is good way to memorize things like :

There are another very good example for that:

Lambda Expressions

The Lambda function called 匿名函数，of course it’s different from def statement.

It goes like that:

1
lambda <parameters>: <return expression>

eg::arrow_down:

1
2
3
4
5
6
>>> square = lambda x: x*x
>>> square
<function <lambda> at 0x00000257213E1DC0>

>>> square(4)
16

When we go square = lambda x: x*xand then call the square we can know that the square function in not square function ,its not like the def statement. Here are the different between these two:

image-20220622161601483

One example code as below:

Logical Operators

To evaluate the expression <left> and <right>:

  1. Evaluate the subexpression <left>.
  2. If the result is a false value v, then the expression evaluates to v.
  3. Otherwise, the expression evaluates to the value of the subexpression <right>.

To evaluate the expression <left> or <right>:

  1. Evaluate the subexpression <left>.
  2. If the result is a true value v, then the expression evaluates to v.
  3. Otherwise, the expression evaluates to the value of the subexpression <right>.

A conditional expression has the form:

1
<consequent>  if  <predicate>  else  <alternative>

Evaluation rule:

  1. Evaluate the <predicate> expression.
  2. If it’s a true value, the value of the whole expression is the value of the <consequent>.
  3. Otherwise, the value of the whole expression is the value of the <alternative>.
1
2
3
>>> x = 0
>>> abs(1/x if x != 0 else 0)
0

Some Resources

Environment Diagram Cheat Sheet

img

week 3&4

Decorators

Python provides special syntax to apply higher-order functions as part of executing a def statement, called a decorator. Perhaps the most common example is a trace.

1
2
3
4
5
6
7
8
9
10
11
12
>>> def trace(fn):
        def wrapped(x):
            print('-> ', fn, '(', x, ')')
            return fn(x)
        return wrapped
>>> @trace
    def triple(x):
        return 3 * x
    
>>> triple(12)
->  <function triple at 0x102a39848> ( 12 )
36

In this example, A higher-order function trace is defined, which returns a function that precedes a call to its argument with a print statement that outputs the argument. The def statement for triple has an annotation, @trace, which affects the execution rule for def. As usual, the function triple is created. However, the name triple is not bound to this function. Instead, the name triple is bound to the returned function value of calling trace on the newly defined triple function. In code, this decorator is equivalent to:

1
2
3
>>> def triple(x):
        return 3 * x
>>> triple = trace(triple)

Recursive Function

Actually it’s nothing new to thec++, so I just be simple, see the code below:

:star: How to check the fact function is correct:

  1. Verify the base case.
  2. Treat fact as a functional abstraction!
  3. Assume that fact(n-1) is correct.
  4. Verify that fact(n) is correct .

One interesting staff about recursive is: Tree Recursion, one good example is Fibonacci numbers:

The process is like the picture below:

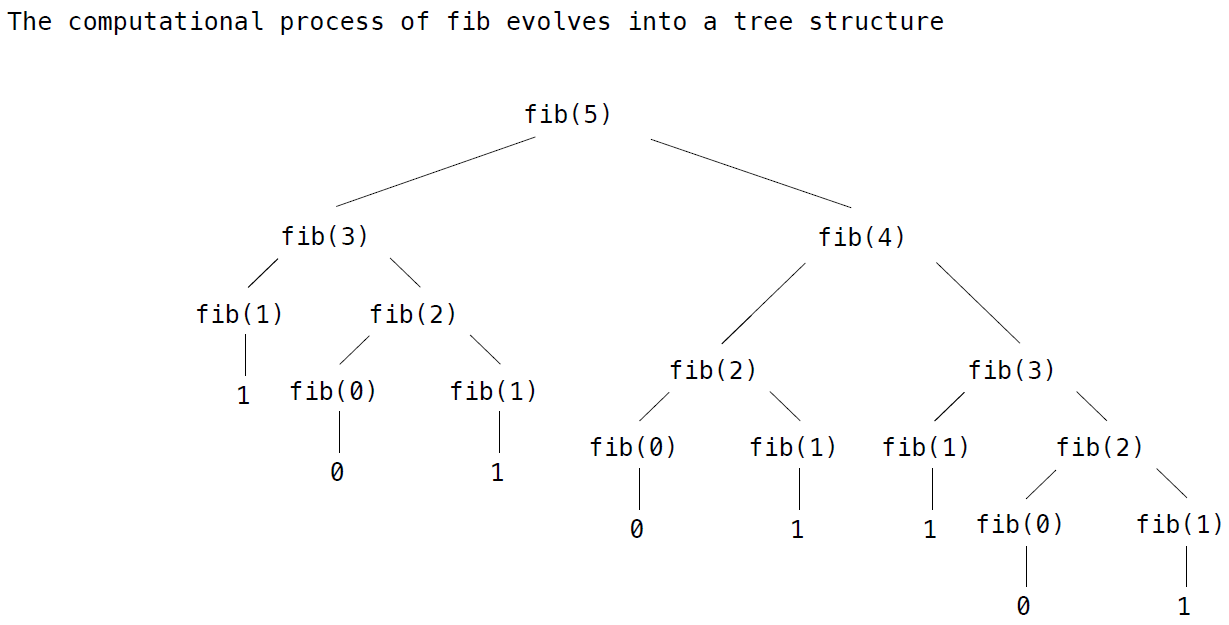
image-20220630173631058

This way to compute the fib number is so inefficiency because if we let the computer to compute the fib(100).It takes so so long. fib is called on the same argument multiple times.

week 5

List

Finally，we got the list. Likes this:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
>>> digits = [1, 8, 2, 8]
>>> digits = [2//2, 2+2+2+2, 2, 2*2*2]

# To get the number of elements
>>> len(digits)
4

#An element selected by its index:
>>> digits[3]
8

>>> from operator import getitem
>>> getitem(digits, 3)
8

# Concatenation and repetition:
>>> [2, 7] + digits * 2
[2, 7, 1, 8, 2, 8, 1, 8, 2, 8]
>>> add([2, 7], mul(digits, 2))
[2, 7, 1, 8, 2, 8, 1, 8, 2, 8]

# Nested lists
>>> pairs = [[10, 20], [30, 40]]
>>> pairs[1]
[30, 40]
>>> pairs[1][0]
30

The basic roles for the list, is quite like the c++,so I will talk more about the new things in python.

Containers

The definition of the containers is Built-in operators for testing whether an element appears in a compound value.

SEE THE EMAMPLE:

1
2
3
4
5
6
7
8
9
>>> digits = [1, 8, 2, 8]
>>> 1 in digits
True
>>> 8 in digits
True
>>> 5 not in digits
True
>>> not(5 in digits)
True

For Statement

Finally , we come to the forstatement.It’s quite different from the c++.A for statement consists of a single clause with the form:

1
2
for <name> in <expression>:
    <suite>

A for statement is executed by the following procedure:

  1. Evaluate the header <expression>, which must yield an iterable value.
  2. For each element value in that iterable value, in order:
    1. Bind <name> to that value in the current frame.
    2. Execute the <suite>.

This execution procedure refers to iterable values. Lists are a type of sequence, and sequences are iterable values. Their elements are considered in their sequential order.

A good example for this statement:

1
2
3
4
5
6
7
8
9
>>> pairs = [[1, 2], [2, 2], [2, 3], [4, 4]]
>>> same_count = 0

>>> for x, y in pairs:
        if x == y:
            same_count = same_count + 1

>>> same_count
2

:star: The way to use a list to create a list is like this:

1
2
3
4
>>> letters = ['a', 'b', 'c', 'd', 'e', 'f', 'm', 'n', 'o', 'p']

>>> [letters[i] for i in [3, 4, 6, 8]]
['d', 'e', 'm', 'o']

More complex is add if, so we get full version of this:

1
2
3
4
[<map exp> for <name> in <iter exp> if <filter exp>]

# Short version: 
[<map exp> for <name> in <iter exp>]

Range

A range is another built-in type of sequence in Python, which represents a range of integers. Ranges are created with range, which takes two integer arguments: the first number and one beyond the last number in the desired range.

1
2
>>> range(1, 10)  # Includes 1, but not 10
range(1, 10)

Calling the list constructor on a range evaluates to a list with the same elements as the range, so that the elements can be easily inspected.

1
2
>>> list(range(5, 8))
[5, 6, 7]

If only one argument is given, it is interpreted as one beyond the last value for a range that starts at 0.

1
2
>>> list(range(4))
[0, 1, 2, 3]

Ranges commonly appear as the expression in a for header to specify the number of times that the suite should be executed: A common convention is to use a single underscore character for the name in the for header if the name is unused in the suite:

1
2
3
4
5
6
>>> for _ in range(3):
        print('Go Bears!')

Go Bears!
Go Bears!
Go Bears!

This underscore is just another name in the environment as far as the interpreter is concerned, but has a conventional meaning among programmers that indicates the name will not appear in any future expressions.

Slicing

Sequences contain smaller sequences within them. A slice of a sequence is any contiguous span of the original sequence, designated by a pair of integers. As with the range constructor, the first integer indicates the starting index of the slice and the second indicates one beyond the ending index.

In Python, sequence slicing is expressed similarly to element selection, using square brackets. A colon separates the starting and ending indices. Any bound that is omitted is assumed to be an extreme value: 0 for the starting index, and the length of the sequence for the ending index.

1
2
3
4
5
6
7
8
9
10
11
12
13
>>> odds = [3, 5, 7, 9, 11]
>>> list(range(1, 3))
[1, 2]
>>> [odds[i] for i in range(1, 3)]
[5, 7]
>>> odds[1:3]
[5, 7]
>>> odds[1:]
[5, 7, 9, 11]
>>> odds[:3]
[3, 5, 7]
>>> odds[:]
[3, 5, 7, 9, 11]

String

String can be anything, just like c++. Of course, in the video there are some brand new features. See the code below:

1
2
3
4
>>> 'curry = lambda f: lambda x: lambda y: f(x, y)'
>>> exec'curry = lambda f: lambda x: lambda y: f(x, y)'
>>> curry
<function <lambda> at XXXXX>

In that case even thought we we use a string but still we can exec it to make it executable.

However , the in and not in operators match substrings:

1
2
3
4
5
6
>>> 'here' in "where's Waldo?"
True
>>>234 in [1,2,3,4,5]
False
>>>[2,3,4] in [1,2,3,4,5]
False

We can see that the List and the string are quite different when we use the in

Another thing that need to pay a lot attention is that we should use "xxx" in a sentences when there exists ' in a sentence.

Dictionaries

Dictionaries are Python’s built-in data type for storing and manipulating correspondence relationships. A dictionary contains key-value pairs, where both the keys and values are objects. The purpose of a dictionary is to provide an abstraction for storing and retrieving values that are indexed not by consecutive integers, but by descriptive keys.

The dictionary type also supports various methods of iterating over the contents of the dictionary as a whole. The methods keys, values, and items all return iterable values.

1
2
>>> sum(numerals.values())
66

A list of key-value pairs can be converted into a dictionary by calling the dict constructor function.

1
2
>>> dict([(3, 9), (4, 16), (5, 25)])
{3: 9, 4: 16, 5: 25}

Dictionaries do have some restrictions:

  • A key of a dictionary cannot be or contain a mutable value.
  • There can be at most one value for a given key.

A useful method implemented by dictionaries is get, which returns either the value for a key, if the key is present, or a default value. The arguments to get are the key and the default value.

1
2
3
4
>>> numerals.get('A', 0)
0
>>> numerals.get('V', 0)
5

Dictionaries also have a comprehension syntax analogous to those of lists. A key expression and a value expression are separated by a colon. Evaluating a dictionary comprehension creates a new dictionary object.

1
2
>>> {x: x*x for x in range(3,6)}
{3: 9, 4: 16, 5: 25}

Processing Container Values

  • sum(iterable[, start]) -> value
    Return the sum of a ‘start’ value (default: 0) plus an iterable of numbers.

  • max(iterable[, key=func]) -> value
    max(a, b, c, …[, key=func]) -> value

    With a single iterable argument, return its largest item.
    With two or more arguments, return the largest argument.

  • all(iterable) -> bool
    Return True if bool(x) is True for all values x in the iterable.
    If the iterable is empty, return True.

Tree

The Tree is kind of an data abstraction,normally it have to kind of format:

  • Recursive description (wooden trees):
    1. A tree has a root label and a list of branches and each branch is a tree.
    2. A tree with zero branches is called a leaf.
    3. A tree starts at the root.
  • Relative description (family trees):
    1. Each location in a tree is called a node
    2. Each node has a label that can be any value
    3. One node can be the parent/child of another
    4. The top node is the root node

How to present a tree is like below:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def tree(label, branches=[]):
    for branch in branches: #Verifies the tree definition
        assert is_tree(branch), 'branches must be trees'
    return [label] + list(branches) #Creates a list from a sequence of branches

def label(tree):
    return tree[0]

def branches(tree):
    return tree[1:]

def is_tree(tree):
    if type(tree) != list or len(tree) < 1:# Verifies that tree is bound to a list
        return False
    for branch in branches(tree):
        if not is_tree(branch):
            return False
    return True

def is_leaf(tree):
    return not branches(tree)

Processing a leaf is often the base case of a tree processing function.
The recursive case typically makes a recursive call on each branch, then aggregates.

1
2
3
4
5
6
7
8
9
def count_leaves(t):
    """The number of leaves in tree.
    >>> count_leaves(fib_tree(5))
	8
	"""
	if is_leaf(t):
	    return 1
	else:
	    return sum([count_leaves(b) for b in branches(t)])

Some other function about trees:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def print_tree(t, indent=0):
    """Print a representation of this tree in which each label is
    indented by two spaces times its depth from the root.

	>>> print_tree(tree(1))
	1
	>>> print_tree(tree(1, [tree(2)]))
	1
	  2
	>>> print_tree(fib_tree(4))
	3
	  1
	    0
	    1
	  2
	    1
	    1
	      0
	      1
	"""
	print('  ' * indent + str(label(t)))
	for b in branches(t):
	    print_tree(b, indent + 1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def print_sums(t, path_sum):
    """Print the sum of labels along the path from the root to each leaf.

    >>> print_sums(tree(3, [tree(4), tree(5, [tree(6)])]), 0)
    7
    14
    >>> print_sums(haste, '')
    has
    hat
    he
    """
    path_sum = path_sum + label(t)
    if is_leaf(t):
        print(path_sum)
    else:
        for branch in branches(t):
            print_sums(branch, path_sum)

week 6

Object